0
Фев 14
Коллеги, приветсвую!
Стоит задача написать программу для решения системы линейных уравнений для определения порисотсти.
В солвере это реализовано функцией Optimization, в которую зашита эта методика. В техлоге тоже есть алгоритм.
По сути, это несовместная система линейных уравнений, которая не имеет единственного решения и весовыми коэффициентами можно настроить, какому уравнению ты больше доверяешь.
Не знаю, как это можно реализовать математически. Может у кого есть подобная программа на любом языке или ссылка на подобный алгоритм. Планирую написать на Пайтоне, но если кто поможет с алгоритмом, на пайтоне я реализовать смогу.
Опубликовано
03 Фев 2014
Активность
20
ответов
6237
просмотров
7
участников
2
Рейтинг



http://habrahabr.ru/post/183220/
В питоне есть либа для этого - sympy.org .
>>> from sympy import *
>>> solve([x - y + 2, x + y - 3], [x, y])
{x: 1/2, y: 5/2}
если что, можно и в браузере http://www.wolframalpha.com/input/?i=x+%2B+y+%3D+5%2C+x+-+y+%3D+1
http://www.wolframalpha.com/input/?i=x%5E2+%2B+y+%2B+z+%3D+6%2C+x+-+y%5E3+%2Bz+%3D+100%2C+x%2By%2Bz%3D1
П-навигатор, давайте уточним задачу. СЛАУ может содержать N уравнений и M неизвестных. Если N == M и система не вырождена, решение единственно. Если кол-во N уравнений меньше чем кол-во M неизвестных, то либо решений нет, либо их бесконечное кол-во. Я правильно поянл, что у вас обратный случай, когда кол-во уравнений больше чем кол-во переменных? Если так, то нужно смотреть на метод наименьших квадратов и подобные методы http://en.wikipedia.org/wiki/Overdetermined_system
Данный пример в sympy выдает первый устраивающий tolerance (1e-15) ответ в зависимости от начальных значений для поиска. Если подставить ответы, то например в первом случае получается наибольшая точность в третьем уравнении.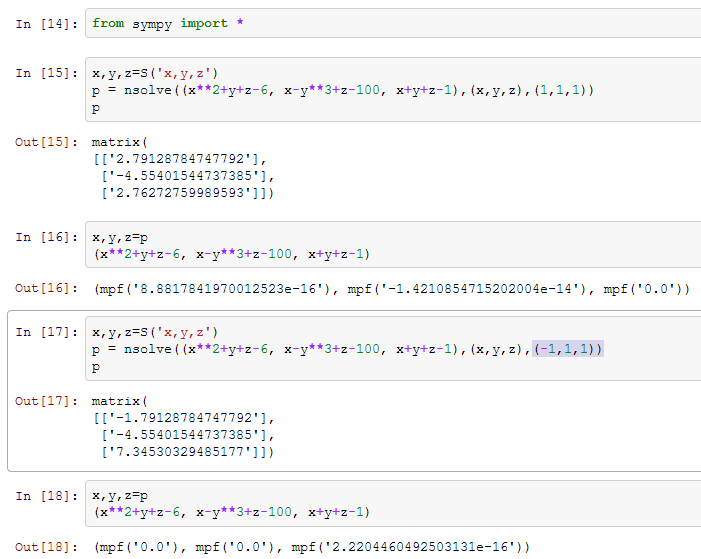
а чтобы не были приблизительные значения - "exact forms" нажать не пробовали? ))
для избыточных вольффрам просто графики показывает
http://www.wolframalpha.com/input/?i=2x%2By%3D-1%2C-3x%2By%3D-2%2C+-x%2By%3D1
http://www.wolframalpha.com/input/?i=155x+%2B+145y+%2B+180z+%3D+166%2C+2.6x+-+2.85y+%2B2.75z+%3D+2.7%2C+0.01x-0.05z%3D1
Получаются результаты приближенные и если увеличить значимость какого либо уравнения, то ответы будут другие.
Так вот мне и нужно меня весовые коэффициенты, получать результаты, при условии, которые я задал изначально.
P-Navigator,
в питоне библиотек для таких задач много, большинство методов оптимизации уже написаны, например в scipy http://docs.scipy.org/doc/scipy/reference/optimize.html или http://openopt.org. Весовые коэффициенты также можно задать во многих методах.
Что то вы меня запутали P-Navigator :) У мнея на работе wolframalpha не работает, но если не ошибаюсь у вас такая система:
155 x + 145 y + 180 z = 166
2.6 x -2.85 y + 2.75 z = 2.7
0.01 x -0.05 z = 1
Если я помню правильно, оно должно иметь единственное решение, поскольку ситема неоднородная, квадратнаая и определитель основной матрицы не равен нулю.
Вот решение
x1=190996/10011
x2=8422/10011
x3=-810104/50055
http://www.math.odu.edu/~bogacki/cgi-bin/lat.cgi?c=sys
Системы линейных уравнений решаются в один проход (методом наименьших квадратов) на основании решения системы dFmin/d ai =0
где Fmin= sum (fi^2) - функция оценки (собственно ошибка)
модули Quanti.Elan в Техлог , MS в Interactive Petrophisics решают нелинейные системы (формулы нелинейных частей известны - большинство методов требуют расчёта первой и второй производных, все решения построены методом наименьших квадратов)
из самых быстрых наверное Levenberg–Marquardt
http://www2.imm.dtu.dk/pubdb/views/edoc_download.php/3215/pdf/imm3215.pdf
ограничения на результирующие переменные тоже задаются как часть системы со своими весами обычно большими (кстати, это не значит, что они в результате будут соблюдены - в документации техлога есть рекомендация задавать минимум для воды 0.01 иначе возможен вылет, собственно на функции Арчи-Дахнова при попытке взять логарифм от отрицательного значения)
PS: в вышеперечисленных программах задаются не весовые коффициенты а обратные им велечины, т.е. вес=1/<то что указывается>(обычно указывают погрешности метода, тогда общая функция ошибки будет общую погрешность выдавать - если вы взаимокорелирующие уравнения решать не будете)
Зачем так мучатся когда есть ELAN?
Не у всех есть ELAN, да и устарел он уже прилично
Всем спасибо за помощь! Попробую реализовать
в древности пользовался методом сопряженных градиентов. в книге "Численные методы" Вержбицкого очень много методов рассмотрено.
Если вы проектный институт, то есть смысл ознакомиться с данными пакетами/библиотеками - реализация на разных языках (программирования), готовые решения для всех вышеперечисленных в топике проблем. Я частенько пользуюсь ими "для различных нужд", очень доволен, т.к. надо только подать входные данные и "забрать" результат.
для русских: http://alglib.sources.ru/equations/linear.php
для "нерусских": http://www.alglib.net/equations/linear.php